固有ベクトル、主成分分析、共分散、エントロピー入門
目次
線形変換 主成分分析(PCA) 共分散行列 基底変換 エントロピーと情報の取得 とにかくコードが欲しい方へ その他の参考資料
本稿は固有ベクトルと行列との関係性について、平易な言葉で、数学にあまり詳しくなくても分かるように書いてみました。この発想に基づいて、PCA、共分散、情報エントロピーについても説明します。
固有ベクトルは英語で「eigenvector」ですが、このeigenはドイツ語で、「そのものだけが持つ」という意味です。例えばドイツ語の「mein eigenes Auto」は、「ほかならぬ私が持つ車」というニュアンスです。このようにeinenは、2つのものの間に存在する特別な関係性を意味します。独特、特徴的、その性質を端的に示すものということです。この車、このベクトルは、私だけのもので、他の誰のものでもありません。
線形代数でいう行列は、スプレッドシートのように数値を2次元に配置した配列で、括弧でくくった一連のスカラー値です。正方行列(例えば2行2列、3行3列など)には固有ベクトルが含まれ、それぞれの行列に特別な関係性があります。これは、ドイツ人が車に対してこだわりを持っているのと少し似ています。
線形変換
というわけでその関係性の定義に入りますが、その前にちょっと脱線して、そもそも行列でどんなことができるのか、行列は他の数値とどう関係するのかという点を説明します。
行列は便利なものです。行列に対しては足し算や掛け算ができるからです。ベクトルvに行列Aを掛けると、新たなベクトルbが得られます。この時、行列に対して入力ベクトルで線形変換を実行したともいいます。
Av = b
この式は、ベクトルvの写像として別のベクトルbが得られることを示しています。
具体的な例で説明します(ここで実行する行列の掛け算を点乗積またはドット積といいます。この演算の詳細については、この記事を参照してください。)
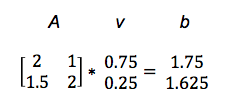
こうしてAをvと掛けることで、bを得ました。以下のグラフは、行列によって、下の方にある短いベクトルv を、上の方にあるベクトルbに写像した様子を表しています。
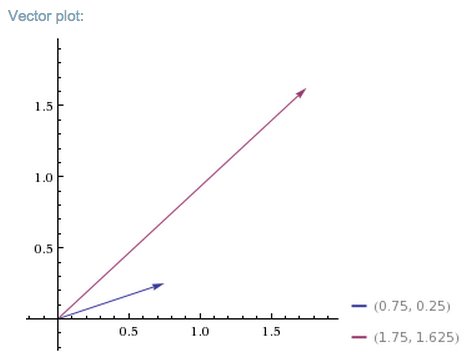
行列Aに対して正のベクトルを次々に与えると、それぞれのベクトルは右上方向に伸びたような新しい空間へ写像されていきます。
入力ベクトルvが全て、通常の格子状の座標空間にあると想像してください。こんな感じです。
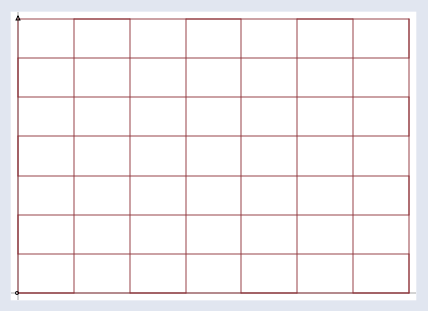
行列により、上図の格子は以下に示す新しい空間に写像され、その中に出力ベクトルbが存在します。
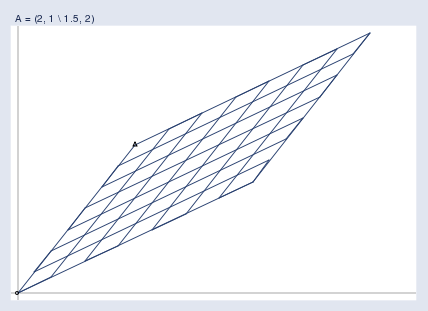
2つの空間が並置されている様子を以下に示します。
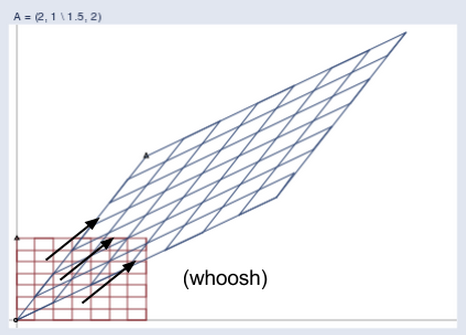
(出典: William Gould、Stata Blog)
行列が1つの空間から別の空間に変換される様子をアニメーションで示すと以下のようになります。
ここで青い線は固有ベクトルを示しています。
行列とは一陣の風だと考えることもできます。目に見えない結果を生む、目に見えない力です。一陣の風は、ある一定の方向に吹きます。固有ベクトルは、行列(風)が吹くその方向を示します。

(出典: Wikipedia)
だとすると、ある空間に吹いている(投射された)行列の影響を受けた全てのベクトルの中で、どれが固有ベクトルなのでしょうか。向きが変わらないものが固有ベクトルです。つまり、行列を「ベクトルの向きを変える風」と考えた時、その風がベクトルを変化させる方向をあらかじめ示しているのが固有ベクトルにあたります。固有ベクトルとは、風向計のようなものです。いわば独特の風向計です。
従って固有ベクトルの定義は、「行列に対応するベクトルで、これが存在することにより、行列をスカラー値係数と同様に扱えるようになるもの」です。この式で、Aは行列、xはベクトル、λはスカラー値係数を示します。スカラー値係数には5や37といった数値、またはπが当てはまります。
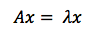
また固有ベクトルは、入力ベクトルを伸長させたり縮小させたりして線形変換を実行する際の軸となる、ともいえます。(変換によって得られる)より大きな行列の振る舞いを表す、変化の路線、まさに線形変換の「芯」です。
ここで私が「軸」(axes)と「路線」(lines)を複数形で示したところに注意してください。ドイツ人が普段の買い物にはVolkswagen、出張の時にはMercedes、遊びで遠出する時にはPorscheというように車を目的によって使い分けるのと同じで、正方行列は行列の次元数と同じ数の固有ベクトルを持つことができます。即ち2行2列の行列なら固有ベクトルは2つ、3行3列なら3つ、n行n列ならn個、となり、それぞれが1つの次元での変換の方向を示します。1
固有ベクトルは、行列の入力値を移動させる際の基準となる力の軸を抽出するので、行列の分解の際に役立ちます。つまり行列の対角化は、固有ベクトルに従って実行します。固有ベクトルは行列を表すので、固有ベクトルはここで、ディープニューラルネットワークでオートエンコーダが展開するタスクと同じものを実行していることになります。
以下にYoshua Bengioの言葉を引用します。
数学的なオブジェクトは、学者同士で議論する際に使う表現ではなく、1つ1つの構成要素に分解するか、そのオブジェクトの特質の中で普遍的なものに注目すれば、より分かりやすくなるものが多い。
例えば、整数は素因数に分解することができる。12という数字の表現方法は、この表記の前提が10進数か2進数かによって変わるが、12 = 2×2×3は常に正しい。
この表現から、12は5によって割り切れないあるいは12の倍数は3で割り切れると言うような、役立つ性質を結論付けることができる。
素因数分解することで整数の本質の何かを発見することができるように、行列を分解することによって、単に行列を表す要素の配列の形で提示するだけでは分かりにくい行列の機能特性をあらゆる方向から情報として見ることができる。
最も広く使われている行列分解は固有分解と呼ばれ、行列を固有ベクトルと固有値に分解するものである。
主成分分析(Principal Component Analysis以下PCA)
PCAは画像のような高次元のデータのパターンを探すツールです。機械学習に取り組んでいる研究者は、ニューラルネットワークの前処理のためにPCAを使用することがあります。画像のセンタリングや回転、データのスケーリングなどで、PCAは位置関係を優先する(低分散次元に落としてくれる)ので、ニューラルネットワークの収束速度と結果全体の品質を改善することができます。
PCAを話す前に、基本的な統計の概念(平均、標準偏差、分散、共分散)の意味を明確にし、これらを後で関連付けられるようにしましょう。これらは綿密に関係しています。
平均とは、言葉のとおり、Xの中の全てのxの平均値で、データを足して、データの数nで割って算出します。
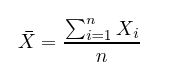
標準偏差は、変に聞こえるかもしれませんが、単に平均値からデータまでの距離を2乗した平均値の平方根です。下の数式では、分子が各データの平均値との違いの和を示し、分母が単にデータの数(引く1)にすることで、平均値からの距離の平均を算出しています。
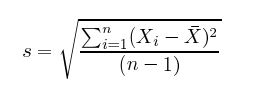
分散はデータのばらつきを計る尺度です。例えば、バスケットボールのオランダ代表選手 を見てみると、チームメンバーの身長はそれほど分散していません。全員身長6フィート(約182cm)以上に分類されるでしょう。
しかし、チームメンバーをやんちゃな幼稚園児のいる教室に入れると、教室にいる全員の身長はかなり分散します。このばらつきが分散であり、この身長の差を表すデータなのです。
分散は単純に言うと、標準偏差の2乗したもので、s^2と表します。
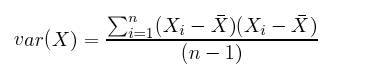
分散も標準偏差もデータと平均値の差を2乗することによって、正の値にするため、平均以上の値と平均以下の値が相殺することがありません。
例えば、個々の年齢(x軸)と身長(y軸)を座標軸で表すと、下のように楕円形に分布します(平均値を0に設定します)。
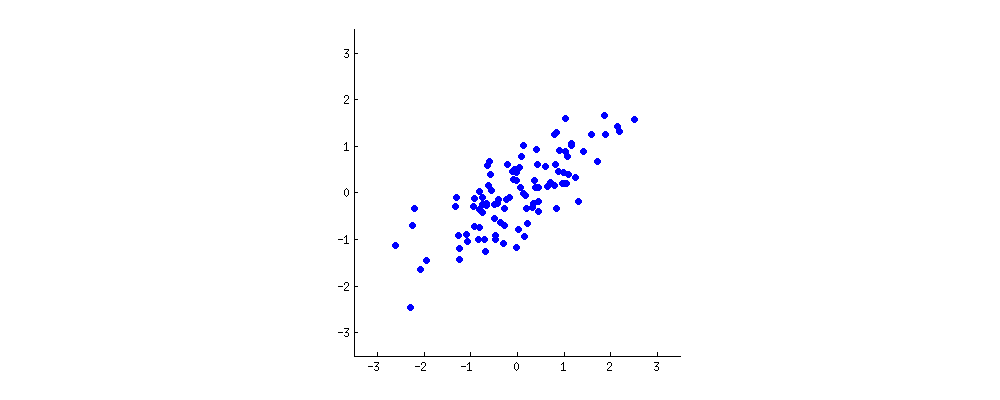
PCAは、直線回帰のように直線を引いてデータを解釈します。
それぞれの線は「主成分」または独立変数と従属変数の関係を示します。データには多数の次元があるように、多数の主成分が存在します。PCAの役割は、その主成分の優先順位を設定することです。
第1の主成分は散乱を直線で両断していて、分散を最もよく説明しています。それぞれの違いを最も良く観察できます。(わずかですが、赤い線で表す部分の情報は失われています。)下のグラフでは、最初の主成分が「バゲット」を横に切っています。
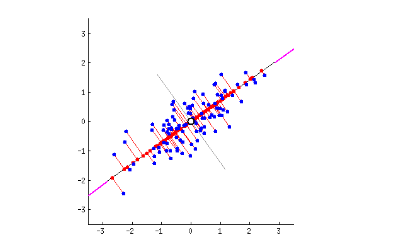
第2の主成分は第1の主成分に垂直に交差して、情報の損失を補っています。上の座標軸では2つの主成分しかありませんが、3次元のデータの場合、第3の主成分を追加することで、第1と第2の主成分から失われた情報を補うことができます。
共分散行列
前述では、行列を「一連のベクトルを変換し、異なる一連のベクトルにするもの」と紹介しましたが、別の考え方もあります。働く力をとらえたデータの表現との考え方もあります。この力は、2つの変数の関係の有無を分散や共分散によって示すものを指します。
データの分散と変数間の共分散を表す数値行列を作成したとします。これが、共分散行列です。これは、観察されたデータの経験的記述です。
共分散行列から固有ベクトルや固有値を見つけることは、データの分散に主成分の直線を当てはめることと同じことです。なぜでしょう。それは、固有ベクトルは主線の力の跡を表し、最大の分散と共分散の座標軸はデータが最も変動しやすい位置を示しているからです。
次のように考えてみてください。変数が変化した場合、確認されているあるいは未確認のなにかによってその変化を強いられたからなのです。もし、2つの変数が一緒に変化したとなると、大抵の場合は、原因は片方がもう一方を影響したからあるいは両方が同じ隠れた未確認のなにかに影響されたから変化が生じたのだと言えます。
行列による線形変換の時、固有ベクトルは入力に適用される力を表します。行列にデータの分散や共分散が並べられている場合、固有ベクトルは与えられたデータに加えられた力を示します。片方は力を加え、もう片方は加えられた力を示します。
固有値は単に固有ベクトルに付随する係数のことを指します。この係数は座標軸の大きさを表します。この場合、データの共分散の大きさになります。固有ベクトルを持っている固有値の高い値から低い値に整列すると、主成分を重要な順番に並べることになります。
例えば次のような2×2の行列があるとします。
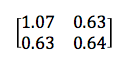
左上の数字と右下の数字がx変数とy変数それぞれの分散を示し、同じく、左下と右上の全く同じ数字がx変数とy変数の共分散を示します。この性質から、対称行列と呼ばれています。見て分かるように、共分散は正の値のため、PCAのセクションの上部の座標軸では線が右肩上がりになっています。
もし、2つの変数が一緒に増減(線が右肩上がり)していれば、共分散は正の値であることになります。しかし、片方が増大するともう片方が減少する場合、共分散は負の値(線が右肩下がり)になります。
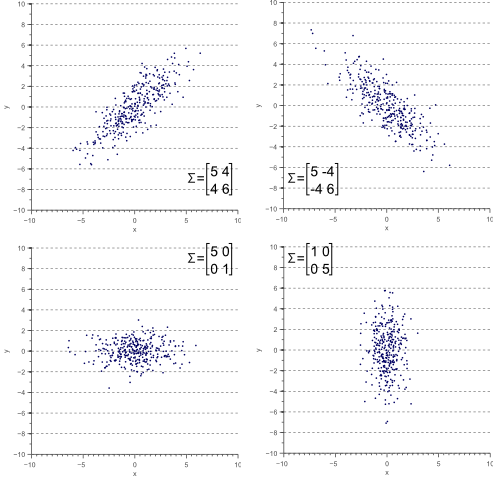
(出典: Vincent Spruyt)
どの変数にも変化がなく、座標に斜め方向の動きがない場合、共分散も全くないことに注意してください。共分散は、2つの変数が一緒に踊るのかを教えてくれます。片方の変数に変化がなく、もう片方に変化がある場合、2つの変数は一緒に踊りません。
次の数式を見れば分散と共分散の違いはわずかであることが分かります。
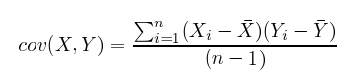 vs.
vs.
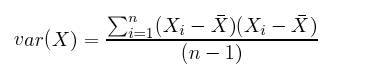
共分散の計算の素晴らしいところは、変数間の関係性が目視できないような高次元空間においても、共分散の値を見ることでその相関性(正の相関、負の相関、無相関)がわかることです。
まとめると、共分散行列はデータの形を定義します。固有ベクトルに沿った斜め方向のばらつきは、共分散によって示され、x軸やy軸に平行したばらつきは分散によって示されます。
統計学においては、統計の中から因果関係を導くことは不評なので、次のことはうのみにしないでください。
正確性には欠けるかもしれませんが、次のように考えでみたらどうでしょうか。上述のバスケットボールのオランダ代表選手を例に挙げると、成分を各選手の力の原因とし、第1主成分を年齢、第2主成分はおそらく性別、第3の主成分を国籍(各国の医療システムの違いを意味)とした場合、それぞれ異なる次元で身長に関連し、それぞれが異なるレベルで身長に影響を与えます。共分散を可能性のある原因を追跡するものとして解釈することができます。
基底変換
共分散行列の固有ベクトルは直交しているため、x軸とy軸からなる座標空間上にあったデータを、新たに主成分を軸とする座標空間上に再設定することができます。最大の分散の線で定義された新しい空間に、データ集合の座標系の基底を新たに定めるのです。
上の図にあるx軸とy軸を行列の基底と呼びます。つまり、xy座標で行列のデータを表現しています。しかし、これを他の座標に沿って別の行列に変換することができます。例えば、行列の固有ベクトルを同じ行列の新たな座標の基底にすることができます。行列とベクトルは生き物であり、xy座標などの特定の座標にある数字には依存していません。
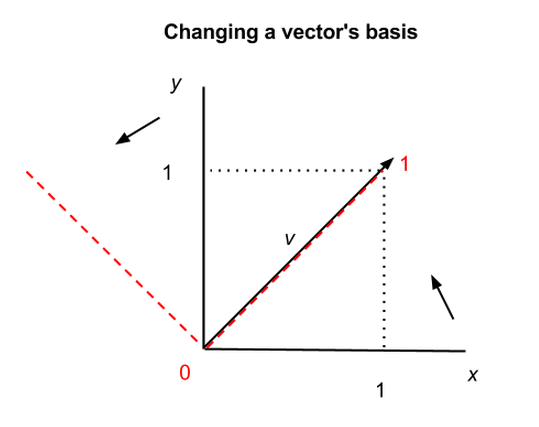
注釈Changing a vector’s basisベクトルの基底変換
上のグラフでは、同じベクトルvを異なる方法で、2つの座標系に置くことができます。xy軸を黒い実線、異なる軸を赤い点線で表しています。第1の座標系では、v = (1,1)で、第2の座標系では、v = (1,0)になりますが、v自体は変わっていません。従って、ベクトルや行列を括弧でくくられた座標値で表現する際は、このようなことが起こります。
これは深く崇高な意味を多く含みます。その1つは、自然の座標は存在せず、n次元空間に存在する数学的オブジェクトは複数の表現に依存しているということです。(行列の基底を変換するとさらに操作しやすくなります。)
ベクトルの基底変換は基数を変更するようなものです。例えば、九という数は10を基数とする表現では9になり、2進法では1001に、3を基数とした場合は30になります(例、1, 2, 10, 11, 12, 20, 21, 22, 30の全てが「九」の異なる表現となります)。同じ数を異なる記号で表せるように、同じベクトルを異なる座標で表すことができるのです。
##エントロピーと情報の取得
情報理論において、エントロピーは持っていない情報を意味します(多くの人は「情報」を持っているものとして定義します。ここでも、例外ではなく、専門用語としては意味が逆であり、十分に知識を持たない人を悩ませています)。システムについて知らない情報、つまりエントロピーは想定外のことに関係します。それが、どれだけ我々を驚かすことでしょう。
例えばコインの両側が表であった場合、何回投げても、必ず表が出るため、コインを投げても得る情報は全くありません。コインを投げなくても表が出ることは分かります。つまり、意外性という要素がない2つの表を持つコインには情報がないと言えます。
バランスのとれたコイン、つまり表と裏があるコインの場合は、コインを投げた時に意外性という要素があります。6面体のサイコロも同じで、意外性は振るたびに大きくなり、どのサイコロの面も同じ確率で出ることになります。これらのどちらも、情報理論において言えば、情報を持っているということになります。
では、今度は細工されたサイコロを使い、6回振ったうち5回も「3」が出た場合、操作されているゲームだろうと見当がつきます。その瞬間、サイコロを振るたびにあった、高揚感は激減します。我々は出るサイコロの面の傾向が分かってしまうのです。
サイコロに細工されたことを理解することは、データ集合で主成分を見つけることに似ています。根底にあるパターンを探し出せばいいのです。
情報が、「私たちがシステムについて知らないこと」から「知っていること」へと移ることは、エントロピーの変化を示します。知見はシステムへのエントロピーを減らします。情報を得て、エントロピーを減すことが、情報の取得なのです。しかも、このタイプのエントロピーは恣意的であり、システムについて知っていることに左右されます。(あくまでも私的意見ですが、情報の取得は、カルバック・ライブラー情報量と同じことだと思います。これについては、別の記事restricted Boltzmann machinesで少しだけ考察しています。)
分布したデータを分析する主成分は、意外性という意味でシステムのエントロピーの減少を示しています。
偶然にも、最大の分散を表する成分からそれぞれの主成分のデータの形を説明するのは、決定木に沿ってデータを説明するのと似ています。PCAの第1主成分は、決定木の最初の決定事項に似ていて、想定外のことを減らしていく次元に沿っています。
とにかくコードが欲しい方へ
ND4Jはn次元配列を扱うJVM向け数値計算ライブラリで、Numpyに主に触発されています。ND4Jがどのように固有ベクトルを扱っているかをご覧いただけます。ND4Jには、JavaとScalaのAPIがあり、HadoopとSparkで実行し、Numpy/Cythonの約2倍も速く大きな行列を処理できます。
その他の初心者用手引
場合によっては、行列に固有ベクトルがフルセットで存在しないかもしれません。行列には、対応する固有値あるいは次元の数だけの線形従属の固有ベクトルが存在できます。