ニューラルネットワークを回帰に使用
一般に、ニューラルネットワークは、教師なしの学習、分類、回帰を目的として使用されます。つまり、教師付きの学習を終えた後、ラベル付けされていないデータをグループ化し、それらのデータを分類し、または連続値を予測します。
分類は、一般に最終層でロジスティック回帰を使い、連続データを0や1などのダミーの変数に変換します。例えば、ある人の身長、体重、年齢の情報を基に心臓病の可能性があるかないかのどちらかに分類します。一方、真の回帰では、あるセットになった連続的入力を別の連続的出力のセットにマッピングします。
例えば、家の築年数とその床面積、いい学校までの距離の情報があると、その家をどのくらいの価格で売ることができるかが予測できるのです。これがある連続データから別の連続データへのマッピングです。分類に使用するような、独立変数xを単に連続的なyにマッピングするダミー変数とは異なります。
分別のある人には回帰にニューラルネットワークを使用することがやり過ぎかどうかについての意見があることでしょうが、ここではそれがどのように行われるのかについてのみを説明します(とても簡単です)。
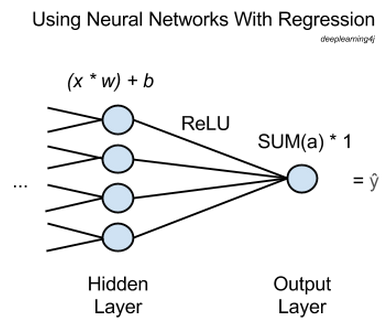
上図では、xは入力、つまりネットワーク内の一つ前の層から前方に通過する特徴を指します。多数のxが、最後の隠れ層の各ノード(節)に入れられ、各々に該当する重みwが掛け合わされます。
そして、これらのxに重みを掛け合わせたものをすべて足し、バイアスを追加した値を活性化関数に入力します。ここで使用する活性化関数は 正規化線形関数 (rectified linear unit、ReLU)といって、一般によく使用されており、非常に役に立つものです。この関数だとシグモイド活性化関数のように浅い勾配で飽和状態になりません。
各隠れノードに正規化線形関数は活性化aを出力し、それらをすべて合計したものが出力ノードまで行き、そのまま通過します。
要するに、回帰を行うニューラルネットワークには、出力ノードが1つあり、このノードでは前の層で活性関数を通過したものの総計に1が掛け合わされるだけなのです。その結果が、ネットワークが推測するŷあるいは”y hat”、つまりすべてのxがマッピングする従属変数となります。
誤差逆伝播法を行い、ネットワークに学習させるには、ŷをyの正解値と比較し、ネットワークの重みとバイアスをエラーが最小限になるまで調整するだけです。その多くは分類器を使って行う作業のようなものです。平均二乗誤差(Root-means-squared-error、RMSE)が損失関数であるかもしれません。
このようにして、ニューラルネットワークを使って任意の数の独立変数xを予測したい従属変数yと関連させる関数を入手することができるのです。
Deeplearning4jのニューラルネットワークを使って回帰を行う場合、多層ニューラルネットワークを設定し、出力層を以下のプロパティの最後に追加します。
//出力層を作成します。
.layer()
.nIn($NumberOfInputFeatures)
.nOut(1)
.activationFunction('identity')
.lossFunction(LossFunctions.LossFunction.RMSE)
nOutは、各層のノード数です。nInは、前層から通過する特徴の数です。つまり、上図の例の場合だと、その値は4となります。activationFunctionは'identity'に設定します。
シンプルな数学的関数を近似させるため、回帰にニューラルネットワークを使ったさらに包括的なサンプルは、こちらをご覧ください。