고유 벡터(Eigenvectors), PCA, 공분산(Covariance) 및 엔트로피(Entropy)에 대한 기초 강의

내용:

선형 변환(Linear Transformations)
주성분 분석(Principal Component Analysis) (PCA)
공분산 행렬(Covariance Matrix)
베이시스 변경(Change of Basis)
엔트로피(Entropy) & 정보 이득(Information Gain)
예제 코드(Just Give Me the Code)
학습 자료

이 포스팅에서는 고유 벡터(eigenvectors) 및 고유 벡터와 행렬과의 관계를 수식 없이 말로 풀어서 설명하려고 합니다. 고유 벡터를 이해하면 공분산(covariance), 주 성분 분석(principal component analysis) 및 정보 엔트로피(information entropy)도 자연스럽게 이해할 수 있습니다.

고유 벡터(아이겐 벡터, eigenvector)의 eigen, 아이겐은 독일어에서 온 말이며, “very own(자기 자신의, 고유의)”라는 뜻 입니다. 예를 들어, 독일어로, “mein eigenes Auto”는 “my very own car(바로 내 자동차)”를 의미합니다

선형 대수학에서 행렬은 직시각형 모양의 2차원 어레이입니다. 직사각 형태의 액셀 스프레드 시트에 각 칸에 각종 숫자가 적혀있는 것을 상상하시면 됩니다. 행렬 중 행과 열의 크기가 같은 행렬을 정방 행렬(square matrix)이라고 합니다. 그리고 모든 정방 행렬은 각 행렬만의 고유한 벡터를 가지고 있습니다. 고유값에 대한 자세한 설명은 이 블로그를 참고하시기 바랍니다.

선형 변환(Linear Transformations)

행렬과 고유 벡터의 관계를 더 자세히 알아보기 전에 잠시 다른 개념을 설명하겠습니다.

행렬을 이용하면 합, 곱 등의 연산을 편리하게 할 수 있습니다. 특히 벡터와 행렬을 이용하면 더욱 복잡한 일을 할 수 있습니다. 어떤 벡터 v에 행렬 A를 곱한 결과가 벡터 b라고 하면, 이를 아래와 같이 나타낼 수 있습니다.

Av = b

즉, 행렬 A를 이용해 벡터 v를 벡터 b로 변환한 것 입니다. 이 과정을 선형 변환이라고 합니다. 혹은 벡터 v를 다른 벡터 b로 매핑(maps)했다고도 합니다.

구체적인 예를 보여드리겠습니다. (행렬 곱이 익숙하지 않으신 분은 여기 또는 이 강의자료(한글)를 참고하시기 바랍니다.)

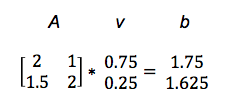
Alt text

이렇게 행렬 A는 벡터 v를 벡터 b로 변환합니다. 어떻게 이 행렬 A가 짧은 파란색 벡터 v를 긴 빨간색 벡터 b에 매핑했는지 아래 그래프에서 확인하시기 바랍니다.

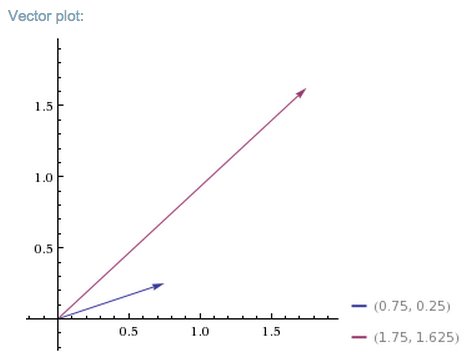
Alt text

이렇게 어떤 벡터든지 행렬 A에 곱해주면 더 높고 멀리 뻗은 새로운 벡터로 매핑이 될 것입니다. 이것을 하나의 공간(space)이 다른 공간(space)으로 투영(혹은 사영, projection)되는 개념으로 설명드리겠습니다.

우선 어떤 입력 벡터 v가 이와 같은 격자 공간(normal grid)에 있다고 상상해 보십시오.

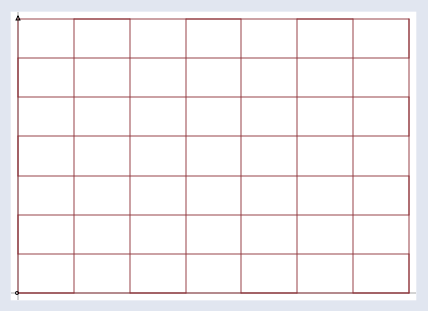
Alt text

그러면 행렬 A는 이 공간을 아래와 같은 공간으로 투영합니다.

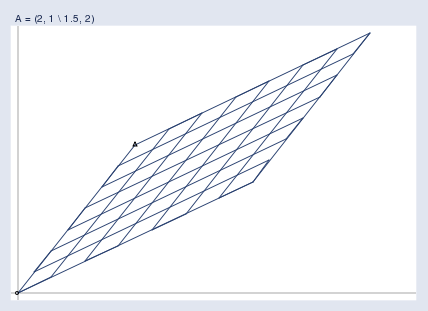
Alt text

두 공간을 같이 그려보았습니다.

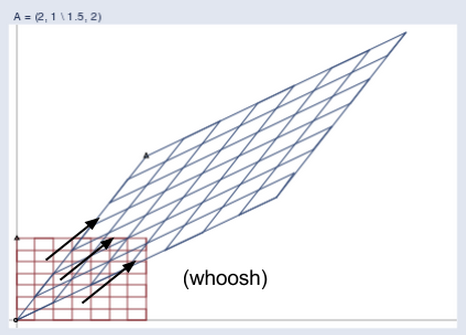
Alt text

(제공: William Gould, Stata Blog)

아래 애니메이션을 보면 더욱 쉽게 이해할 수 있습니다.

이 애니메이션을 보면 다른 벡터와는 달리 파란색 벡터들은 투영 전/후에 방향에 변화가 없는 것을 알 수 있습니다. 투영 전/후에 파란색 벡터 각각의 길이는 늘어나지만 그 방향은 전혀 변하지 않은 상태로 남아있습니다.

이 파란색 벡터의 방향이 변하지 않는 이유는 행렬 A가 벡터를 투영하는 방향과 그 방향이 같기 때문입니다. 이런 벡터를 우리는 고유 벡터라고 부릅니다. 예를 들어 바람이 거세게 불면 풍향계는 바람을 받아서 바람의 방향을 가리키게 됩니다. 만일 풍향계가 원래부터 바람의 방향을 향하고 있었다면 그 풍향계의 방향은 바뀌지 않습니다. 즉, 행렬의 고유벡터는 그 행렬의 방향을 - 바람이 부는 방향을 - 나타냅니다.

Alt text (제공: Wikipedia)

고유 벡터는 행렬 A를 곱하더라도 방향이 변하지 않고 그 크기만 변합니다. 따라서 고유 벡터는 아래 식과 같이 표현할 수 있씁니다. 행렬 A를 좌변에 곱하였지만 그 결과가 마치 어떤 숫자를 벡터에 곱한것과 같은 결과가 나오는 것 입니다. 이 방정식에서, A는 행렬, x는 벡터, lambda는 스칼라 값인 상관 계수(예:5, 37, pi와 같은 숫자) 입니다.

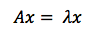
Alt text

다른 관점으로 생각할 수도 있습니다. 선형 변환은 입력 벡터의 크기를 늘이거나 줄이는 경우가 있는데 이 때 고유벡터는 크기를 늘이거나 줄이는 데 기준이 되는 축이라고 할 수 있습니다. 즉 선형 변환의 ‘선’에 해당하는 것이 바로 이 고유 벡터입니다.

그런데 이 고유 벡터는 사실 여러 개가 존재합니다. 정방 행렬은 최대 그 차원수 만큼의 고유 벡터를 가질 수 있습니다. 예를 들어 2x2 행렬은 두 개의 고유 벡터를, 3x3 행렬은 3개의 고유 벡터를 가질 수 있습니다. 1

이렇게 고유 벡터는 행렬이 작용하는 힘의 방향과 관계가 있고, 이 때문에 고유 벡터는 행렬을 분해(decomposition)하는데 사용됩니다. 즉 어떤 행렬 A는 그 행렬의 고유 벡터를 이용해 대각행렬화(diagonalization) 할 수 있습니다. 참고로 이 대각행렬화는 행렬의 정보를 압축해서 표현해주는 것인데, 딥 신경망으로 오토 인코더를 구현하는 것도 같은 목적을 갖고 있습니다.

Yoshua Bengio는 다음과 같이 이를 정리했습니다.

수학적 객체는 그 구성 성분들로 나누어서 생각하거나, 우리가 그 개념을 표현하는 방식과 전혀 관계없는 보편적인 속성을 파악하면 쉽게 이해할 수 있습니다.

예를 들면 어떤 정수(integers)는 그 정수의 소인수(prime factors)로 분해할 수 있습니다. 정수 12를 표현하는 방법은 우리가 그것을 십진법으로 혹은 이진법으로 작성할 것인지에 따라 달라집니다. 그러나 12 = 2 × 2 × 3은 항상 성립합니다.

이 표현에서 우리는 12는 5로 나누어 떨어지지 않는다거나 12의 모든 배수가 3으로 나누어 떨어진다는 것과 같은 유용한 성질을 파악할 수 있습니다.

정수를 소인수로 분해해서 쉽게 숫자의 특징에 대해 이해할 수 있듯이, 행렬도 마찬가지로 여러가지 요소로 분해해서 생각할 수 있습니다.

행렬을 분해하는 방법엔 여러 가지가 있습니다. 그 중에서 가장 널리 사용되는 방법은 행렬을 여러 개의 고유 벡터와 고유 값으로 분해하는 고유 벡터 분해(eigen vector decomposition)입니다.

주성분 분석(PCA, Principal Component Analysis) (PCA)

PCA는 이미지와 같은 고차원 데이터에서 패턴을 찾는 도구 중 하나입니다. 기계학습 알고리즘에서 데이터를 인공 신경망에 입력하기 전의 전처리 과정에서 PCA가 사용되곤 합니다. PCA를 통해 데이터의 범위를 재조정하고 데이터의 평균을 0으로 맞춰줌으로써 PCA는 고차원 데이터 중 중요한 차원을 골라줍니다. 결과적으로 신경망 학습의 수렴 속도와 성능을 향상시킬 수 있습니다.

PCA에 대해 설명하기 위해 우선 통계의 가장 기초적인 개념인 평균, 표준편차, 분산, 그리고 공분산에 대해 설명하겠습니다. 그리고 이 개념을 모두 이해하면 PCA는 아주 간단히 이해할 수 있습니다.

평균(mean)은 모든 데이터의 합을 데이터의 개수 n으로 나누어 구할 수 있습니다. 말 그대로 우리가 갖고 있는 데이터 셋 X에 존재하는 모든 x의 평균 값입니다.

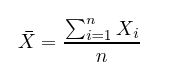
Alt text

표준 편차(Standard deviation)는 각 데이터 x와 평균 사이의 거리를 제곱하고, 이 평균을 구한 뒤, 그 값에 다시 제곱근(square root)을 씌운 값입니다. 아래 식을 참고하면 식의 분자는 각 데이터와 평균값과의 거리를 표현하고 있고, 분모는 전체 데이터의 수에서 1을 뺀 값입니다.

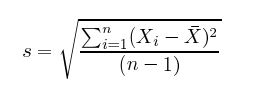
Alt text

분산(Variance)은 데이터가 얼마나 분산되어 있는지, 즉 얼마나 퍼져있는지에 대한 측정값입니다. 예를 들어 네덜란드 농구 팀 선수들의 키 데이터로 분산을 측정한다면 그 값은 그리 크지 않을 것입니다. 왜냐하면 그들은 대부분 190cm 이상의 장신이기 때문입니다.

반대로 그 농구 팀과 유치원생을 섞어놓고 키를 재서 데이터로 쓴다면, 그 데이터의 분산은 아주 클 것입니다. 왜냐하면 데이터에 작은 키와 큰 키가 섞여있기 때문에, 즉 상대적으로 데이터가 더 퍼져있기 때문입니다.

분산은 표준 편차의 제곱과 같고, 종종 s^2로 표현됩니다.

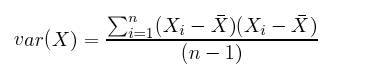
Alt text

분산과 표준 편차의 계산 과정을 보면 둘 다 각 데이터와 평균과의 차이를 제곱합니다. 따라서 분산과 표준편차는 둘다 항상 양수입니다.

이제 예를 들어봅시다. 우리 데이터는 여러 사람의 나이와 키 값이고, 나이를 x축에, 키를 y축에 나타내보겠 습니다. 보기 좋게 x축과 y축이 평균이 0이 되도록 데이터를 이동했다고 하겠습니다.

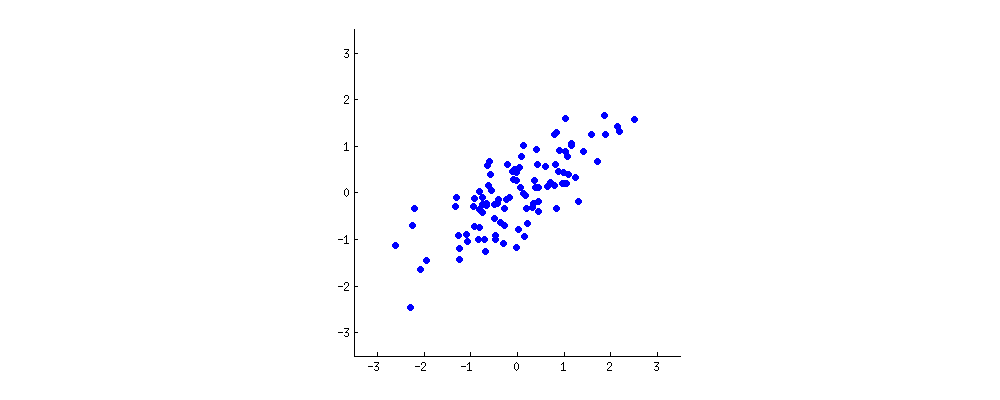
Alt text

PCA는 선형 회귀 분석과 유사하게, 데이터에서 의미있는 ‘선’ 혹은 ‘축’을 찾는 과정입니다.

각각의 축은 하나의 주성분(principal component)에 해당합니다. 데이터에는 차원 수 만큼의 주성분이 존재하는데, 여기서 PCA는 어떤 축이 더 중요한지 그 우선 순위를 구하는 것 입니다.

첫 번째 주성분은 가장 길게, 가장 퍼져있는 방향의 축에 해당합니다. 예를 들어 아래의 그래프를 보면 마치 바게트를 길이 방향으로 길게 자르는 듯한 방향이 데이터의 분산이 가장 큰, 즉 가장 퍼져있는 방향에 해당합니다.

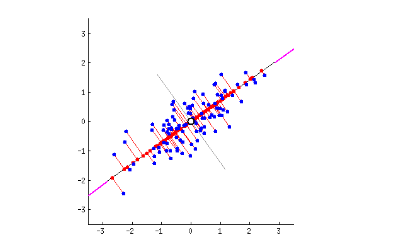
Alt text

두 번째 주성분의 경우 첫번째 주성분으로 표현할 수 없는 축 중에서 가장 분산이 큰 축에 해당합니다. 이 그림의 경우 전체가 2차원 데이터라 두 개의 주성분이 존재합니다. 만일 3차원 데이터라면 3개의 주성분이 존재합니다.

공분산 행렬(Covariance Matrix)

앞에서 행렬의 역할 중 벡터를 변환해주는 역할을 소개했었습니다. 이번엔 조금 다른 관점으로 행렬에 대해 이야기하겠습니다. 행렬을 이용하면 두 밴수가 서로 어떤 관계를 가지는지를 쉽게 표현할 수 있습니다. 특히, 각 데이터의 분산과 공분산을 이용해 만드는 공분산 행렬이 이에 해당합니다.

쉽게 말하자면, 정방 행렬의 값을 각 변수의 분산과 공분산으로 채운 것이 바로 공분산 행렬입니다. 이에 대해서는 이제부터 자세히 설명하겠습니다.

우선 공분산 행렬의 쓰임새에 대해 알아보겠습니다. 공분산 행렬에서 고유 벡터와 고유 값을 찾는 것은 데이터의 주성분을 찾는 것과 동일합니다. 왜냐하면 위에서 언급했 듯이 고유 벡터는 행렬이 어떤 방향으로 힘을 가하는지를 표현하는데, 이것은 데이터가 어떤 방향으로의 분산이 가장 큰지를 구하는 것과 같기 때문입니다.

두 개의 변수가 있다고 생각해보십시오. 변수 하나가 변할 수도 있고 두 변수가 같이 변할 수도 있습니다. 어떻게 되든지 간에 그 이유는 그 데이터가 그렇게 나오도록 하는 원리가 있기 때문일 것입니다.

어떤 행렬로 선형 변환을 하는 경우 고유 벡터는 그 행렬이 벡터에 작용하는 힘의 방향을 나타냅니다. 만일 이 행렬이 공분산 행렬일 경우에 이 공분산 행렬의 고유 벡터는 데이터가 어떤 방향으로 분산되어 있는지, 즉 어떤 방향으로 힘이 작용하는 지를 나타냅니다.

고유값(Eigenvalues)은 각 고유 벡터에 해당하는 상관 계수일 뿐입니다. 우리가 다루는 행렬이 공분산 행렬일 경우 고유 값은 각 축에 대한 공분산 값이 됩니다. 그리고 고유 값이 큰 순서대로 고유 벡터를 정렬하면, 결과적으로 중요한 순서대로 주성분을 구하는 것이 됩니다.

2x2 공분산 행렬의 예는 아래와 같습니다.

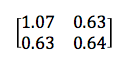
Alt text

좌측 하단 (2,1)성분 및 우측 상단의 (1,2) 성분의 값이 동일합니다. 이 값은 x와 y의 공분산을 포현합니다. ‘x와 y의 공분산’과 ‘y와 x의 공분산’의 값이 같기 때문에 두 값이 동일한 것입니다. 한편 좌측 상단의 값은 x의 분산에, 우측 하단의 값은 y의 분산에 해당합니다. 결과적으로 공분산 행렬은 대각선 성분을 중심으로 대칭이 되게 됩니다. 그리고 PCA 섹션 상단의 데이터 그래프를 보면 데이터가 우상향입니다. 즉, x의 값이 커질수록 y의 값도 커지기 때문에 공분산의 값이 양수입니다.

만일 x의 값이 커질수록 y의 값이 감소하는 데이터라면 공분산 값은 음수가 됩니다.

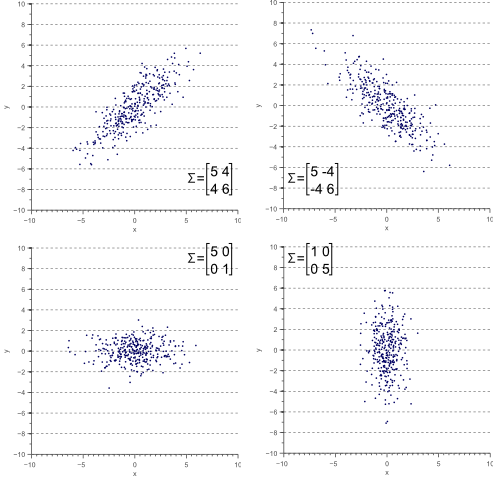
Alt text

(제공: Vincent Spruyt)

만일 변수 x의 변화에 따른 변수 y의 변화가 전혀 없다면, 즉 데이터 그래프가 우상향이나 좌상향이 아닌 경우엔 공분산의 값이 0이 됩니다. 즉, 공분산 값은 두 변수가 연관이 되어있어서 같이 변하는지 아닌지를 알려줍니다.

아래 방정식을 보면 분산과 공분산을 구하는 과정은 거의 차이가 없다는 것을 알 수 있습니다. 예를 들면 ‘x의 분산’은 ‘x와 x의 공분산’이라고 생각할 수 있습니다.

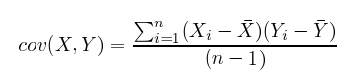
Alt text

vs.

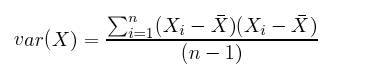
Alt text

공분산은 아주 유용합니다. 고차원 변수의 경우 시각화하기 어렵기 때문에 변수의 상관 관계를 파악하기 어렵습니다. 이럴 때 공분산을 이용하면 각 변수의 값과 부호(음/양)를 통해 변수의 관계를 쉽게 알 수 있습니다. (상관계수(Correlation coefficient)공분산을 -1과 1 사이의 값으로 정규화한 것 입니다.)

요약하자면, 공분산 행렬은 데이터의 분포 형태를 나타냅니다. x축과 y축의 분산은 각 변수의 분산으로 표현되고, 대각선 방향의 분산은 공분산으로 표현됩니다.

통계 자료를 보고 인과 관계를 알아내는 것은 매우 어렵고 아주 많은 경우에 잘못 사용되곤 합니다. 매우, 매우 주의하시기 바랍니다.

위의 네덜란드 농구선수 키 데이터를 인과 관계와 엮어 생각해볼 수 있습니다. 예를 들어 첫 번째 주 성분으로 나이를, 두 번째 주 성분으로 성별을, 세 번째 성분으로 국적을 표현하면 키와 성별, 키와 국적의 관계를 각각의 공분산으로 파악할 수 있고 결과적으로 어떤 인과 관계를 추정해볼 수 있습니다. 그러나 공분산으로 알 수 있는 것은 상관 관계이지, 인과 관계가 아니라는 것을 주의하시기 바랍니다.

기저(basis) 변경

공분산 행렬의 고유 벡터는 서로 수직(orthogonal)입니다. 따라서 이 고유 벡터에 해당하는 축을 이용해 데이터를 나타낼 수 있습니다. 즉 값을 나타내는 좌표계(기저)를 변환하는 것(re-base the coordinate system) 입니다.

그 동안 우리는 기저로 x축과 y축을 사용해 왔습니다. 즉, 그 동안 데이터는 x, y축에서 어떤 값에 해당하는지를 x, y좌표로 나타냈습니다. 그러나 같은 데이터를 다른 축을 이용해서 표현할 수 있습니다. 예를 들면 한 행렬의 고유 벡터를 이용해 각 데이터의 값을 표현할 수 있습니다. 고유 벡터는 서로 수직이기 때문에 모든 데이터를 나타내는 것이 가능합니다.

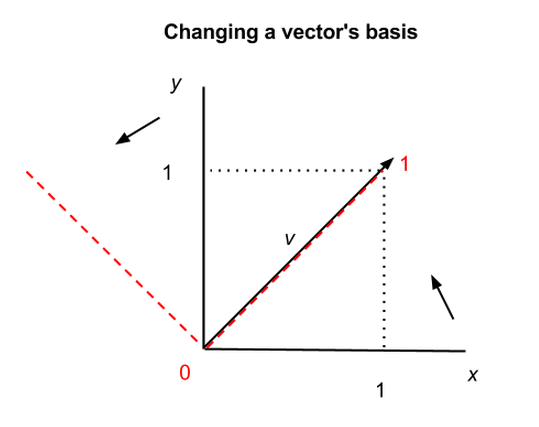
Alt text

위의 그래프에서, 하나의 벡터 v가 어떻게 다른 축을 이용해 표현되는지 볼 수 있습니다. 검정색 축은 x, y축입니다. 한편 붉은색 점선을 이용한 다른 축을 선택할 수도 있습니다. 검정색 축에 의하면 v는 (1,1)이지만 붉은색 축에 의하면 v는 (1,0)이 됩니다. 하지만 v는 여전히 같은 v입니다.

다소 철학적인 이야기인데, 어떤 값이든 그거을 표현하는 방법은 여러 가지 방법이 있고 우리가 일반적으로 쓰는 방법이 유일하지 않다는 것입니다.

다른 기저(basis) 벡터를 이용해 벡터의 값을 표현하는 것은 마치 어떤 진법을 이용해 숫자를 표현하느냐와 비슷합니다. 숫자 9는 십진법에서 9, 이진법에서 1001, 삼진법에서는 30으로 표현합니다. 본질적으로 그 값은 같지만 어떤 방식으로 표현하느냐의 차이가 있을 뿐입니다.

엔트로피 & 정보 이득(Entropy & Information Gain)

정보 이론에서 엔트로피(entropy)란 우리가 가지고 있지 않은 정보의 양을 의미합니다. 즉, 우리가 얼마나 어떤 시스템에 대해, 혹은 변수에 대해 모르고 있는지, 얼마나 실제 관측이 우리를 놀라게 할 수 있는지에 대한 값입니다.

만일 양면이 모두 앞인 동전이 있다고 하면, 이 동전은 여러분에게 아무런 정보를 제공하지 않습니다. 왜냐하면 어떻게 던지든지간에 이 동전은 늘 앞을 보여줄 것 이기 때문입니다. 따라서 이 동전을 아무리 던져도 예상 외의 일이 일어나지 않으며, 우리는 전혀 이 결과를 보고 놀라지 않을 것 입니다. 이런 경우에 정보 이론에서는 이 동전이 아무런 정보를 가지고 있지 않다고 이야기합니다.

한편 양면이 각각 앞/뒤인 동전은 던질 때마다 어느 정도 예상하지 못하는 결과가 나옵니다. 육면체 주사위를 던진다면 더욱 더 예측하기가 어려우며, 따라서 결과는 더욱 우리에게 놀랄 거리를 제공합니다. 정보 이론에서는 이런 동전이나 주사위는 정보를 가지고 있다고 이야기합니다.

주사위를 여섯번 굴렸더니 다섯번이나 3이 나와서, 이 주사위가 사실은 6면 중 하나를 빼면 전부 3으로 이루어져 있다는 것을 알았다고 해봅시다. 이렇게 되면 주사위의 결과는 대부분 3일 것이고, 즉 더 예측 가능한 상태가 되고 우리는 덜 놀랄 것 입니다.

위의 주사위 굴리기 예제는 데이터 셋에서 주성분을 찾는 것과 비슷합니다.

우리가 시스템에 대해 알게 될수록 시스템의 엔트로피는 감소합니다. 예를 들어 데이터의 통계를 알게 되면 엔트로피는 감소합니다. 이것을 정보 이득(information gain)이라고 합니다. (참고로, 정보 이득는 저희가 RBM(Restricted Boltzmann Machines) 튜토리알에서 설명한 Kullback-Leibler divergence와 같습니다.)

데이터의 분포를 주성분으로 나타내면 성분의 차수가 낮아질수록 분산이 감소합니다. 그리고 분산이 낮아진다는 것은 엔트로피가 감소하는 것을 의미합니다.

데이터를 주성분으로 표현하는 것은 결정 트리(decision tree)의 단계를 결정 단계를 밟아나가는 것과 유사합니다. 잘 만들어진 결정 트리는 첫번째 가지의 if-then-else가 가장 대표적인 질문이 되어야 하는데, 이것은 마치 PCA의 첫번째 주성분이 가장 엔트로피를 감소시키는 차원을 고르는 것과 같습니다.