초보자를 위한 RNNs과 LSTM 가이드

내용

이 포스팅은 RNNs(Recurrent Neural Networks), 특히 RNNs의 한 종류인 LSTM(Long Short-Term Memory)을 설명하는 포스팅입니다.

RNNs은 글, 유전자, 손글씨, 음성 신호, 센서가 감지한 데이타, 주가 등 배열(sequence, 또는 시계열 데이터)의 형태를 갖는 데이터에서 패턴을 인식하는 인공 신경망 입니다.

RNNs은 궁극의 인공 신경망 구조라고 주장하는 사람들이 있을 정도로 강력합니다. RNNs은 배열 형태가 아닌 데이터에도 적용할 수 있습니다. 예를 들어 이미지에 작은 이미지 패치(필터)를 순차적으로 적용하면 배열 데이터를 다루듯 RNNs을 적용할 수 있습니다.

RNNs은 배열에 등장했던 패턴을 ‘기억’할 수 있는 능력이 있습니다. 이 부분은 사람의 기억과 기억력에 비유하면 아주 간결하게 설명할 수 있어서 종종 RNNs을 사람의 뇌처럼 취급합니다.1

일반적인 인공 신경망

RNNs을 이해하려면 우선 일반적인 인공 신경망(FFNets)를 이해하셔야 합니다. 일반적인 인공 신경망을 Feed-forward neural networks라고도 하는데 그 이름에서 이미 RNNs (Recurrent neural networks)과 어떤 점이 다른지 드러납니다. FFNets은 데이터를 입력하면 연산이 입력층에서 은닉층(hidden layers)를 거쳐 출력까지 차근차근 진행됩니다. 이 과정에서 입력 데이터는 모든 노드를 딱 한 번씩 지나가게 됩니다. 그러나 RNNs은 은닉층의 결과가 다시 같은 은닉층의 입력으로 들어가도록 연결되어 있습니다.

FFNets의 입/출력이 각각 사진과 사진의 라벨(고양이, 코끼리..)이라면 (즉, 지도 학습의 경우) 이 FFNets은 사진에 있는 물체에서 패턴을 파악해서 적절한 라벨을 찾아줍니다. 아래 그림에 나온 FFNets의 구조를 참고하시기 바랍니다.

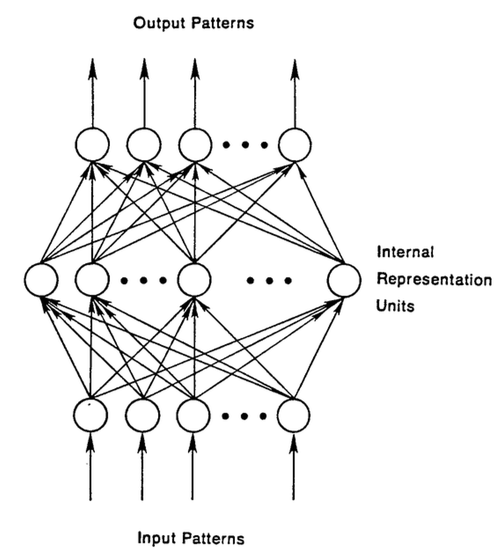
Alt text

FFNets은 라벨을 붙여놓은 이미지 데이터로 학습을 진행하면서 점점 오차를 줄여갑니다. 학습이 이루어지기 전에 데이터의 일부를 따로 관리하는데, 이를 테스트 셋이라고 합니다. 테스트 셋은 학습 과정에서는 사용하지 않습니다. 비유하자면 시험에 나올 문제의 유형과 범위는 알려주지만 출제할 문제는 정확히 알려주지 않는 것입니다. 한편 신경망은 학습 과정에서 사용하는 데이터를 독립적으로 학습합니다. 즉, 데이터의 순서는 중요하지 않습니다.

다시 말해 FFNets은 시간 순서를 무시하고 현재 주어진 데이터만 가지고 판단합니다. 즉, 이 데이터 전에 봤었던 데이터가 무엇인지 기억하려 들지 않습니다. 그야말로 오늘만 사는 FFNets이라고 할 수 있습니다.

RNNs

RNNs은 FFNets과는 좀 다릅니다. RNNs은 지금 들어온 입력 데이터와 과거에 입력 받았던 데이터를 동시에 고려합니다. 아래의 Elman이 제안한 아주 간단한 RNNs의 구조도를 보면, 입력으로 BTSXPE가 들어오는데 은닉층에서는 이 입력데이터와 좌측 하단의 CONTEXT UNIT을 다 입력으로 받습니다.

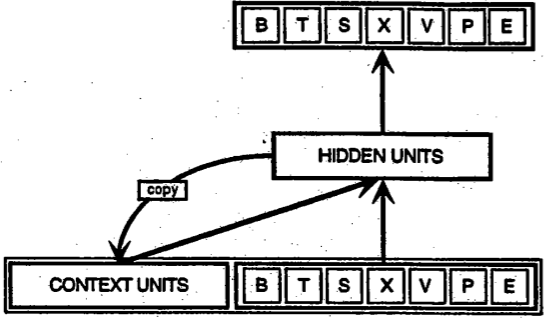
Alt text

t-1시점의 RNNs 출력값은 t시점의 RNNs 출력값에도 영향을 줍니다. 결과적으로 RNNs은 두 개의 입력을 가지고 있는 셈입니다. 하나는 현재 들어온 입력이고,또 하나는 과거의 출력입니다.

과거의 출력이 다시 입력이 되는 구조를 소위 피드백 구조라고 합니다. 피드백 구조는 방금 일어난 출력을 다시 입력으로 집어 넣는데, 이 구조 덕분에 RNNs은 기억 능력이 있다고 합니다.2 인공 신경망이 기억 능력을 넣는 이유는 일반적인 인공 신경망이 할 수 없는 일 때문입니다. 배열의 정보를 보유하고 이 정보를 이용해 원하는 일을 하게 하는 것 입니다.

배열의 정보는 RNNs의 은닉층에 저장됩니다. 이 은닉층에 보관한 정보는 시간이 지난 뒤에 저장한 정보가 필요한 입력이 들어오면 다시 사용됩니다.

마치 머릿속에 기억을 저장하고 있듯이 RNNs은 은닉층에 기억을 저장합니다. 사람은 생각하고 판단하는 과정에서 과거의 기억에 의존하는데, RNNs이 하는 일도 이와 비슷합니다.

이제 이 작동 과정을 수식을 이용해 살펴보겠습니다.

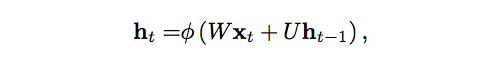
Alt text

시간 t에서 은닉층의 상태, 즉 은닉층이 갖고 있는 값을 h_t라고 하겠습니다. 이 값은 같은 시점 t에 들어온 입력 x_t와 계수 행렬 W, 시간 t-1에서 은닉층의 값 h_t-1, 그리고 h_t와 h_t-1의 관계를 나타내는 행렬 U의 함수입니다. (이 행렬 U는 Markov 체인의 상태 전이 행렬(transition matrix)과 비슷합니다.) 계수 W는 지금 들어온 입력과 보유하고 있던 기억(은닉층의 값)이 얼마나 중요한지 판단하는 값입니다. 예를 들어 W가 아주 큰 값으로 이루어져 있다면 기억하고 있는 h는 별로 중요하지 않고, 현재 들어온 입력값 x_t를 위주로 판단을 내립니다. FFNets과 마찬가지로 출력단에서 오차를 계산하고 이 오차는 다시 이 은닉층으로 내려오는데, 그 값을 기준으로 W업데이트합니다.

입력 x와 기억 h의 합은 함수 φ를 통과하면서 압축됩니다. 보통 tanh나 로지스틱 시그모이드(logistic sigmoid)를 사용합니다. 이 함수는 출력값의 범위를 제한해주면서 전 구간에서 미분 가능하기 때문에 backprop이 잘 적용됩니다.

여기에서 h_t와 h_t-1의 피드백은 매순간마다, 즉 모든 t마다 이루어집니다. 그런데 h_t의 값을 구하기 위해선 h_t-1이 필요하고, h_t-1의 값을 구하는데는 다시 h_t-2가 필요합니다. 결과적으로 은닉층은 과거의 h를 전부 기억하고 있어야 하는데, 실제로 값을 무한히 저장할 수는 없으므로 사용 가능한 메모리 등 여러 상황에 맞추어 적당한 범위까지만 저장을 합니다.

예를 들어 RNNs이 문자열을 입력받으면, 우선 첫 번째 문자로 학습을 하고 학습한 내용을 은닉층에 저장합니다. 그리고 이 값을 이용해 두 번째 입력을 처리합니다. 예를 들면 q 다음엔 u가 올 확률이 높고, t다음엔 h가 올 확률이 높은데, 이 정보를 이용할 수 있습니다.

RNNs은 애니메이션으로 시각화하면 쉽게 이해할 수 있습니다. 아래 애니메이션을 참고하시기 바랍니다. 혹시 그림이 뜨지 않는다면 이 링크를 누르세요.

how recurrent neural networks work #deeplearning4j #dl4j

애니메이션에서 x는 입력, w는 입력 데이터에 곱해지는 가중치, a는 은닉층의 활성값(=입력과 은닉층 값을 고려해서 구해지는 값), b는 은닉층이 sigmoid 함수를 통과한 출력입니다.

BPTT:Backpropagation Through Time (시간을 거슬러 가는 backprop)

RNNs의 목적은 배열 (시계열) 데이터를 분류하는 것이라고 말씀드렸습니다. 그리고 RNNs의 학습은 다른 인공 신경망의 학습과 마찬가지로 오차의 backprop과 경사 하강법(Gradient Descent)을 사용합니다.

FFNets의 backprop은 출력단에서 구한 오차를 신경망을 거슬러 가면서 각 계수를 업데이트 하는 것 입니다. 여기서 각 계수가 출력단의 오차에 얼마나 기여하는지를 계산하고 그 기여도 만큼 업데이트를 하게 됩니다. 기여도는 편미분 ∂E/∂w으로 계산합니다. 그리고 이 값을 사용해 각 계수를 얼마나 증가 혹은 감소시킬지 결정합니다.

RNNs은 backprop의 확장판인 BTPP(Backpropagation Through Time)(https://www.cs.cmu.edu/~bhiksha/courses/deeplearning/Fall.2015/pdfs/Werbos.backprop.pdf)을 사용해 계수를 학습합니다. 본질적으로 BTPP는 기본적인 backprop과 똑같습니다. 다만 RNNs의 구조가 시간에 따라 연결되어 있기 때문에 backprop역시 시간을 거슬러 올라가며 적용되는 것 뿐입니다.

인공 신경망은 RNNs이든 FFNets이든 결국 여러 함수의 조합입니다. f(g(h(x)))같은 계산을 어떤 식으로 수행하는지만 다를 뿐이고 여기에 시계열 데이터를 위해 피드백이 추가되더라도 본질은 연쇄 법칙(chain rule)에 따른 backprop입니다.

Truncated BPTT: 단기 BPTT

Truncated BPTT은 시간 전체를 거슬러 올라가는 BPTT를 간략화 한 것입니다. 시계열 데이터가 길어지면 은닉층에 저장해야 하는 양이 계속 늘어나기 때문에 모든 시간에 대한 은닉층의 값을 저장하는 것은 현실적으로 불가능합니다. 따라서 적당한 선에서 타협을 한 것이 바로 단기 BPTT입니다. 단기 BPTT를 사용하면 기준 길이보다 오래된 값은 반영하지 않으므로 RNNs의 기억력이 짧아지는 문제가 있습니다.

그라디언트 안정화 문제 (Vanishing (and Exploding) Gradients)

RNNs의 역사는 제법 깁니다. 1980년대에 이미 RNNs에 대한 논문이 여럿 나왔습니다. 그리고 1990년대 초반에 그라디언트 소실(vanishing gradient)이라는 문제가 나타났습니다.

gradient의 개념은 아주 단순합니다. x-y평면에 직선을 그으면, 직선의 미분값은 정의에 따라 x의 작은 변화량에 따른 y의 변화량의 비율을 나타냅니다. 이를 인공 신경망에 적용하면 신경망의 모든 가중치와 오차의 관계를 구할 수 있습니다. 즉, 신경망의 값을 얼만큼 변화시키면 그 결과로 오차가 어떻게 변하는지를 알아낼 수 있습니다. 따라서 gradient의 계산은 아주 중요합니다. 만일 gradient를 잘 구할 수 없다면 계수와 오차의 관계를 알 수가 없고, 결과적으로 학습이 잘 되지 않습니다.

RNNs은 시간을 거슬러 올라가며 과거 은닉값을 추적합니다. 그런데 이 추적이 이어질수록 - 즉 과거로 많이 거슬러 올라가면 - gradient의 계산이 잘 되지 않는 경우가 있습니다.

이것은 신경망이 곱하기 연산을 기반으로 이루어져있기 때문입니다.

은행의 적금 상품을 보면 1보다 아주 조금만 큰 값이라도 여러 번 곱하면 나중엔 제법 큰 값이 됩니다. 복리의 마법이라고도 하는데, 적은 이율로도 아주 오랜 기간을 보관하면 나중엔 엄청난 금액이 됩니다. 마찬가지로 1보다 아주 살짝 작은 값이라도 계속 곱하게 되면 나중엔 0에 가까운 값이 됩니다.

인공 신경망의 연산도 많은 곱하기로 이루어져 있고, 계속 곱해나가다보면 그라디언트가 완전 소실되거나(vanishing) 발산하는(exploding) 경우가 있습니다.

그라디언트가 발산하는 경우엔 최종적으로 컴퓨터가 다를 수 있는 가장 큰 숫자를 넘어서버립니다. 그러나 발산은 비교적 제어하기가 쉽습니다. 그라디언트의 최대 범위를 지정해주면 됩니다. 문제는 바로 그라디언트가 소실되는 경우입니다.

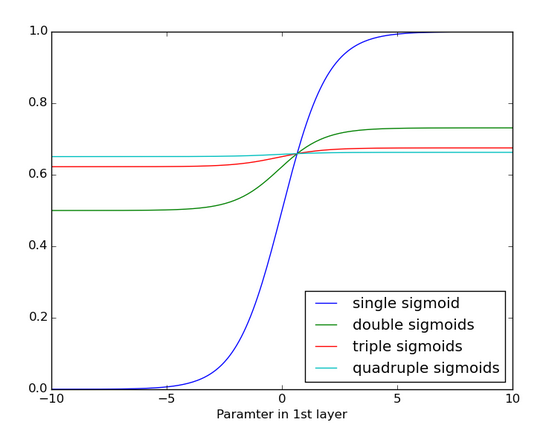
아래 그래프를 보면 시그모이드를 여러 번 곱하면 어떻게 되는지 알 수 있습니다. 딱 네 번 곱했을 분인데 굉장히 함수가 굉장히 평평해집니다. RNNs의 backprop도 마찬가지입니다. 이렇게 평평해지면 기울기가 거의 모든 구간에서 0에 가까워집니다. 즉, 그라디언트가 제대로 전파 되지 않습니다.

Alt text

Long Short-Term Memory Units (LSTM)

RNNs의 변형인 LSTM(Long Short-Term Memory) 유닛은 90년대 중반에 처음으로 등장했습니다.

LSTM은 오차의 그라디언트가 시간을 거슬러서 잘 흘러갈 수 있도록 도와줍니다. backprop하는 과정에서 오차의 값이 더 잘 유지되는데, 결과적으로 1000단계가 넘게 거슬러 올라갈 수 있습니다. 이렇게 그라디언트가 잘 흘러간다는 것은 다시 말해 RNNs가 더 오래 전 일도 잘 기억한다는 의미입니다.

LSTM유닛은 여러 개의 게이트(gate)가 붙어있는 셀(cell)로 이루어져있으며 이 셀의 정보를 새로 저장/셀의 정보를 불러오기/셀의 정보를 유지하는 기능이 있습니다(컴퓨터의 메모리 셀과 비슷합니다). 셀은 셀에 연결된 게이트의 값을 보고 무엇을 저장할지, 언제 정보를 내보낼지, 언제 쓰고 언제 지울지를 결정합니다. 이 게이트가 열리거나(1) 닫히는(0) 디지탈이 아니라 아날로그라는 점 주의하셔야 합니다. 즉, 각 게이트는 0에서 1사이의 값을 가지며 게이트의 값에 비례해서 여러 가지 작동을 합니다.

각 게이트가 갖는 값, 즉 게이트의 계수(또는 가중치, weight)는 은닉층의 값과 같은 원리로 학습됩니다. 즉 게이트는 언제 신호를 불러올지/내보낼지/유지할지를 학습하며 이 학습과정은 출력의 오차를 이용한 경사 하강법(gradient descent)을 사용합니다.

아래 그림은 LSTM 유닛과 게이트의 작동 방식을 시각화한 것 입니다.

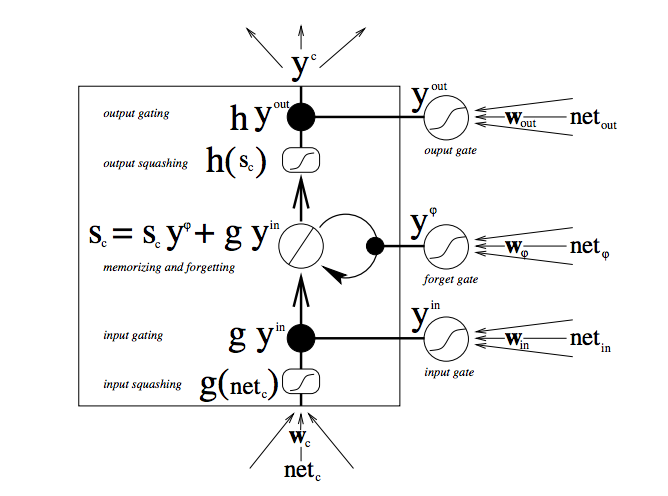
Alt text

LSTM의 구조는 간단하지 않습니다. 만일 LSTM을 처음 공부하신다면 이 다이어그램이 단번에 이해되진 않을 것입니다. 차근차근히 살펴보시길 바랍니다.

우선 그림의 맨 아래 입력부터 보겠습니다. 3개의 화살표는 LSTM유닛에 입력되는 신호입니다. 이 신호는 현재 입력신호와 과거의 셀에서 온 피드백을 합친 것인데, 바로 입력되는 것이 아니라 3개의 게이트로 들어가고 각 게이트에서는 입력값을 어떻게 다룰 것인지를 정합니다.

그림에서 검은색 점은 게이트를 나타냅니다. 아래에 있는 게이트는 얼마나 입력값을 반영할지, 중간의 게이트는 현재 갖고있는 값 중 얼마를 잊을지, 위에 있는 게이트는 얼마나 출력할지를 결정합니다. S_c는 현재 LSTM유닛의 셀의 상태이고 g_y_in은 셀에 입력되는 값입니다. 모든 게이트는 샘플마다, 즉 매 시점마다 얼마나 열고 닫을지를 결정한다는걸 기억하십시오.

(그림에서 크게 써있는 문자가 각 게이트의 값을 반영한 결과입니다.)

아래 그림은 LSTM을 다른 방식으로 시각화한 것 입니다. 왼쪽의 유닛이 기본적인 RNNs의 유닛이고 오른쪽이 LSTM의 유닛입니다(파란 점선과 실선은 무시하세요).

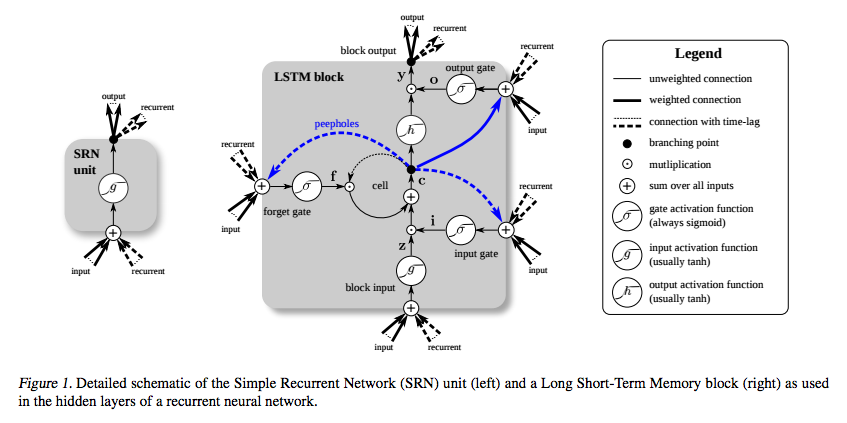
Alt text

굉장히 복잡하지만 제일 중요한 것은 LSTM블록의 중간에 있는 더하기(+) 기호입니다. 일반적인 RNNs의 유닛은 곱하기로만 이루어져있는데, LSTM은 피드백을 더하기로 잇고 있습니다. 따라서 위에서 이야기한, sigmoid를 곱하다 보니 생기는 그라디언트 소실 문제가 없는 것 입니다.

3개의 게이트(입력/출력/망각 게이트)는 각자 다른 가중치를 가지고 있으며 그 값으로 각 게이트에 입력으로 들어오는 값을 조절합니다. ???

망각 게이트의 bias를 1로 설정하는 팁을 활용하면 성능을 증가시킬 수도 있습니다. (한편 Sutskever는 bias를 5로 설정하라고 권고한 바 있습니다.)

기억력을 오래 보존하는 것이 목적인데 왜 LSTM은 망각 게이트를 가지고 있는 걸까요? 쉽게 설명하면 때론 잊는 것이 좋을 때가 있기 때문입니다. 예를 들어 읽던 문서가 다 끝나고 다음 문서를 다루기 시작하는 경우엔 기억을 싹 지우고 새로 시작하는 것이 더 정확할 수 있습니다.

아래 그림은 각 단계마다 다른 게이트가 작동하는 모습을 그린 것입니다. 직선은 닫힌 게이트, 동그라미는 열린 게이트입니다. 그리고 은닉층의 노드에 위/왼쪽/아래의 게이트가 각각 출력/망각/입력 게이트입니다.

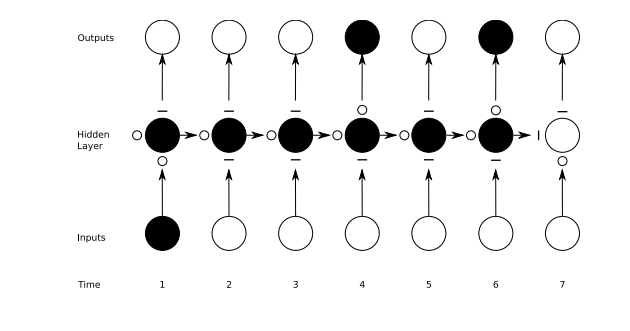
Alt text

마지막으로 RNNs과 FFNets의 아주 큰 차이를 간략히 언급하면, FFNets은 입력 하나에 출력 하나, 즉 입력:출력이 1:1입니다. 그런데 RNNs은 설정하기에 따라 일대일, 일대다(이미지 설명하기), 다대다(기계 번역), 다대일(음성신호 인식) 등 다양하게 적용할 수 있습니다.

다양한 시간 단위의 시계열 데이터 분석

LSTM의 작동 과정에서 정확히 어떤 값이 입력되면 유닛의 쓰기 게이트가 열리고 닫히는지, 또 출력 게이트가 열리고 닫히는지, 즉 어떤 사건에 게이트가 어떻게 열리고 그 구체적인 과정이 잘 와닿지 않을 것입니다. 우선 이 쓰기/읽기 게이트은 LSTM을 다양한 규모의 시계열 데이터에도 반응하도록 해준다는 점을 알려드리겠습니다.

사람의 인생에 이 과정을 비유해봅시다. 삶은 다양한 시계열 데이터로 이루어져있습니다. 예를 들어 지금 여러분의 지리적 위치는 여러분의 1초 뒤의 위치와 매우 큰 관련이 있습니다. 이런 경우엔 게이트가 항상 열려있을 것입니다.

한편 여러분이 부모님께 매 주말마다 전화를 드린다고 하면 이 전화를 드리는 사건과 여러분의 위치와는 큰 관계가 없습니다.

또, 4년마다 국회의원 선거에 투표를 하는데 이 투표라는 사건과 부모님께 드리는 전화, 그리고 본인의 지리적 위치는 서로 거의 영향을 주지 않습니다.

이렇게 시계열 데이터엔 여러가지 일이 동시에 일어납니다. 음악엔 여러 리듬이 섞여있고 글에는 다양한 주제가 등장하며 주식 시장은 각종 요인에 의해 요동칩니다. 이런 여러 사건은 동시에, 다른 시간 주기로 일어나며 LSTM은 이런 여러가지 요인을 잘 잡아냅니다.

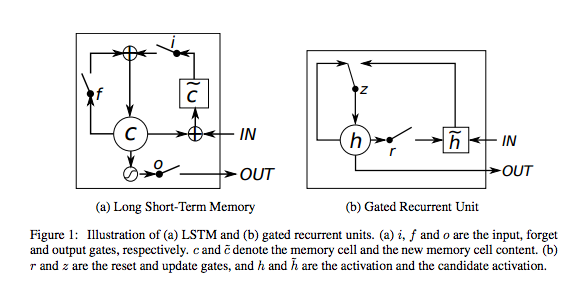
Gated Recurrent Units (GRUs)

RNNs 유닛의 한 종류로 GRU(Gated Recurrent Units)이 있습니다. GRU는 LSTM과 유사하지만 출력 게이트를 생략한 형태이며 따라서 항상 메모리에서 결과를 출력합니다.

Alt text

예제 코드

Graves LSTM 예제를 보면 어떻게 셰익스피어의 작품을 학습하고 모방하는지 잘 나와있습니다. 특히 주석이 잘 달려있으니 코드를 보시면 이해할 수 있습니다. DL4J에서 구현되었으며 API 문법이 불분명한 경우엔 모두 주석이 달려있습니다. 혹시 질문이 있다면 저희의 Gitter 대화에서 문의주십시오.

팁: LSTM 하이퍼파라미터 정하기

LSTM의 하이퍼파라미터를 정하는 팁을 몇 가지 적어놓았으니 참고하십시오.

  • 과적합(overfitting)이 일어나는지를 계속 모니터링하십시오. 과적합은 신경망이 학습 데이터를 보고 패턴을 인식하는 것이 아니라 그냥 데이터를 외워버리는 것인데 이렇게 되면 처음 보는 데이터가 왔을 때 제대로 결과를 내지 못합니다.
  • 학습 과정에서 규제(regularization)가 필요할 수도 있습니다. l1-규제, l2-규제, 드롭아웃을 고려해보십시오.
  • 학습엔 사용하지 않는 시험 데이터(test set)를 별도로 마련해두십시오.
  • 신경망이 커질수록 더 많고 복잡한 패턴을 인식할 수 있습니다. 그렇지만 신경망의 크기를 키우면 신경망의 파라미터의 수가 늘어나게 되고 결과적으로 과적합이 일어날 수 있습니다. 예를 들어 10,000개의 데이터로 수백만개의 파라미터를 학습하는 것은 무리입니다.
  • 데이터는 많으면 많을수록 좋습니다.
  • 같은 데이터로 여러 번 학습을 시켜야합니다.
  • 조기 종료(early stopping)을 활용하십시오. 검증 데이터(validation set)를 대상으로 얼마나 성능이 나오는지 확인하면서 언제 학습을 끝낼 것인지를 정하십시오.
  • 학습 속도(learning rate)를 잘 설정하는 것은 중요합니다. DL4J의 ui를 써서 학습 속도를 조절해보십시오. 이 그래프를 참고하십시오.
  • 다른 문제가 없다면 레이어는 많을수록 좋습니다.
  • LSTM에서는 하이퍼탄젠트보다 softsign함수를 사용해보십시오. 속도도 더 빠르고 그라디언트가 평평해지는 문제(그라디언트 소실)도 덜 발생합니다.
  • RMSProp, AdaGrad, Nesterove’s momentum을 적용해보십시오. Nesterove’s momentum에서 시작해서 다른 방법을 적용해보십시오.
  • 회귀 작업에서는 데이터를 꼭 정규화하십시오. 정말 중요합니다. 또, 평균제곱오차(MSE)를 목적 함수로 하고 출력층의 활성함수(activation function)은 y=x(identity function)을 사용하십시오. (역자 주: 회귀 작업이라도 출력값의 범위를 [0,1]로 제한할 수 있다면 binary cross-entropy를 목적 함수로 사용하고 출력층의 활성함수는 sigmoid를 사용하십시오.)

학습 자료 (영어)

DL4J의 다른 튜토리알

그 외

각주

1) RNNs과 인공 지능은 생각보다 유사합니다. RNNs 알고리즘이 좋기도 하지만 사실 사람의 지능과 기억력은 생각보다 단순합니다. 피드백 루프로 구현된 ‘기억력’은 인간의 의식을 구성하는 필수 요소입니다. 물론 다른 요소도 필요합니다. 예를들어 데이터를 보고 어떤 결정을 내리는 논리 구조는 강화 학습(reinforcement learning)으로 구현이 가능합니다. 이미 구글 딥마인드는 강화 학습을 이용한 인공지능을 선보였습니다.

2) 학습된 인공 신경망은 종류에 관계없이 ‘기억력’이 있습니다. 하지만 FFNet에서는 그 기억력이 더 업데이트되지 않고 고정됩니다. 하지만 RNNs은 학습 과정끝난 뒤에도 입력 데이터에 따라 계수가 바뀝니다. 비유로 설명하면, 어렸을때 처음으로 빨간색, 파란색이 어떤 색깔인지 알게 되면 그 기억은 변하지 않습니다. 하지만 5분전에 지나간 차 색깔이 무슨 색이었는지를 물어보면 대부분 기억하지 못할 것입니다. 단기기억은 사라지기 때문입니다. 한편 언어를 습득하고 나면 문장을 어떻게 이해하는지 배우게 되는데 이 과정은 문장에서 단어가 어떤 순서로 등장했는지를 해석하는 과정입니다. 문장은 핵심적인 정보와 불필요한 부가정보가 같이 섞여있는데 사람이 자연스럽게 이를 해석하는 과정은 RNNs이 시계열 데이터를 해석하는 과정과 유사합니다.

지터에 대해 우리와 채팅하십시오