神经网络与回归
总体而言,神经网络的用途包括无监督学习、分类和回归。具体来说,这些用途分别指将未标记的数据聚类、判定数据的类别以及在有监督定型后对连续值进行预测。
分类网络的最终层通常包含某种形式的逻辑回归算法,用于将连续数据转换为形如0和1的虚拟变量(例如,根据一些人的身高、体重和年龄判断他们是否属于心脏病高危人士),而真正意义上的回归算法则用于将一组连续的输入映射至另一组连续的输出。
比方说,给出一幢房子的年龄、建筑面积和这幢房子到好学校的距离,根据这些信息来预测房子的售价——从连续输入到连续输出。这种情况下并不存在分类问题中的虚拟变量,而是直接将自变量x映射至一个连续的y。
对于将神经网络用于回归算不算高射炮打蚊子这个问题,人们看法不同,各有道理。本页的目的仅仅是介绍具体做法(很容易)。
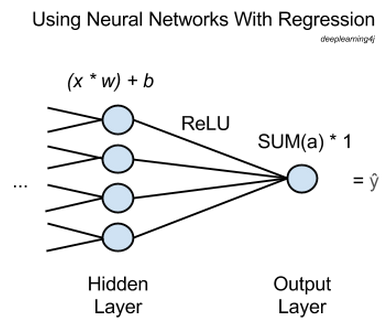
在上图中,x表示输入,即从网络前一层向前传递而来的特征。许多个x将被输入最后一个隐藏层的各个节点,每个x都会与一个相应的权重w相乘。
节点中的所有乘积之和再与一项偏差相加,结果输入某种激活函数。此处的激活函数是一个修正线性单元(ReLU),ReLU很常用也很有用,因为它不会像sigmoid激活函数发生那样饱和区梯度过于平缓的问题。
ReLU会输出每个隐藏节点对应的激活值a,所有激活值之和再进入输出节点并直接通过该节点。
也就是说,用于进行回归的神经网络有一个输出节点,而该节点只会将前一层的激活值之和乘以1。所得结果为ŷ(读作“y hat”),这是网络的预测结果,也是所有x映射至的应变量。
若要让网络通过反向传播进行学习,只需要比较ŷ与y的实际基准值,不断调整网络的权重和偏差,直至预测误差最小化——就和分类器的学习方式一样。损失函数可选用均方根误差(RMSE)。
如此一来,您就可以用神经网络来获取将任意自变量x关联至所要预测的应变量y的函数了。
若要在Deeplearning4j中用神经网络来进行回归预测,您需要建立一个多层神经网络,再在最后添加一个具备以下属性的输出层:
//创建输出层
.layer()
.nIn($NumberOfInputFeatures)
.nOut(1)
.activationFunction('identity')
.lossFunction(LossFunctions.LossFunction.RMSE)
nOut是层中的节点数量。nIn是从前一层传递来的特征数量——上图所示的网络中应为4。activationFunction(激活函数)应设为'identity'(恒等)。
我们还有更完整的神经网络回归示例,能够模拟一些简单的数学函数。